This chapter comes from Mike Grabarek’s new book Fast Track Astrologer

27         Celestial Geometry

 

When you enter birth information into an astrology software program, a Natal chart magically appears. The Natal chart is a two-dimensional (2-D) picture of a particular configuration in the three-dimensional (3-D) cosmos. It's useful to understand the 3-D cosmological picture and to draw connections with the 2-D Natal chart. I know many of you cringe at the thought of geometry, so we will proceed slowly, step by step.

In this chapter, we will determine all the House Cusps. First we will find the Cardinal House Cusps, which are the 1^st House Cusp (Ascendant A^s), 4^th House Cusp (Imum Coeli I^c), 7^th House Cusp (Descendant D^s), and 10^th House Cusp (Midheaven, Medium Coeli M^c). There is agreement with all House systems for determining all four of these Cardinal House Cusps. The variety of House systems in use employ various methods to determine the intermediate House Cusps: 2^nd, 3^rd, 5^th, 6^th, 8^th, 9^th, 11^th, and 12^th. We'll use the Krusiński House system to determine the intermediate House Cusps.

 

Four Seasons

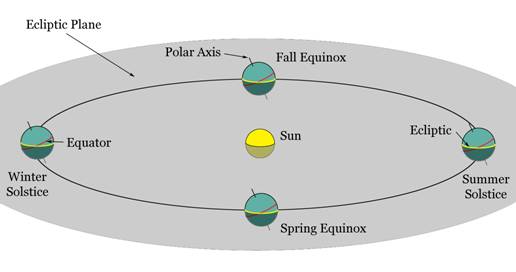
Let's begin by viewing the Earth revolving around the Sun. In the diagram below, we can see positions of the Earth during the equinoxes and solstices. The plane formed by the Earth revolving around the Sun is called the Ecliptic plane. Notice that it slices the Earth into two equal hemispheres. The circle formed around the Earth's surface by the Ecliptic plane is called the Ecliptic.

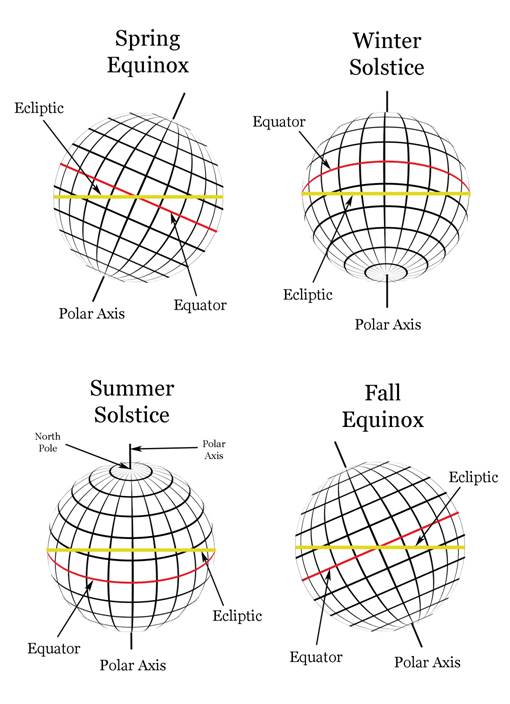
Next we will move our vantage point to the center of the Sun and see what the Earth looks like during the solstices and equinoxes. This is shown in the diagram below. Because we are viewing the Earth from the Sun, the portions of the Earth you can see below are receiving daylight while the back sides of the Earth are in darkness. During the winter solstice, the North Pole is in darkness and the South Pole receives sunlight all day. During the summer solstice, the North Pole receives sunlight all day while the South Pole remains in darkness.

View of the Earth from the Center of the Sun

 

We will gradually construct a celestial diagram of the Earth when viewed from the center of the Sun. The birth will be on May 5, 1990 at 10:45 am in Washington, DC, U.S.A.

We will begin by viewing the Earth from the perspective of the Sun on May 5, 1990. This is shown in the figure below.

Because we are viewing the Earth from the center of the Sun, the entire front side of the Earth is receiving sunlight while the back side is experiencing night time. May 5^th is past the spring equinox, so we would expect the North Pole to be lit 24 hours a day as the Earth spins around its polar axis. You can see this is the case as the North Pole is visible in the diagram below.

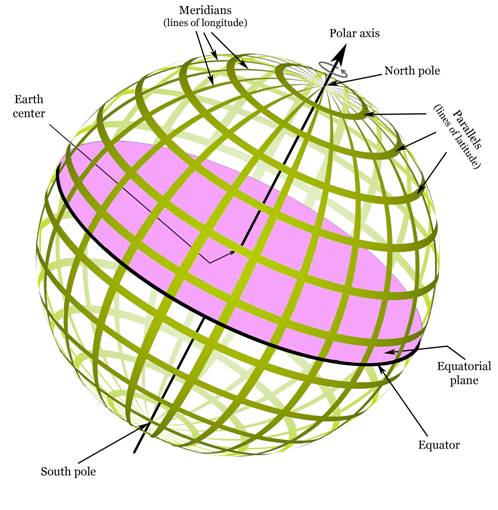
Viewing the polar axis from above the North Pole, the Earth rotates counterclockwise. Over a period of 24 hours, the Earth will rotate completely around its polar axis.

I'd like to also point out the meridians (lines of longitude), which run north-south, and the parallels (lines of latitude), which run east-west.

Finally, we see that the equatorial plane slices the Earth into two equal-sized hemispheres that form the equator at the earth's surface.
 

 

 

 

Ecliptic

Next, we will add one new feature to the diagram: the Ecliptic. As you saw in the first diagram above, the Ecliptic plane is the plane formed by the Earth revolving around the Sun. This sweeping movement of the Earth from the Sun's perspective will form a flat plane, which we call the Ecliptic plane.

The Ecliptic plane slices the Earth into two equal halves, and thus goes through the Earth's center. The line formed around the earth's surface by the Ecliptic plane is called the Ecliptic.

The diagram below has the Ecliptic added. Because we are viewing the Earth from the center of the Sun, the Ecliptic appears as a straight horizontal line slicing the Earth into two equal hemispheres. Just as the equatorial plane goes through the  earth's center, so does the Ecliptic plane.
 

 

 

Birth Location

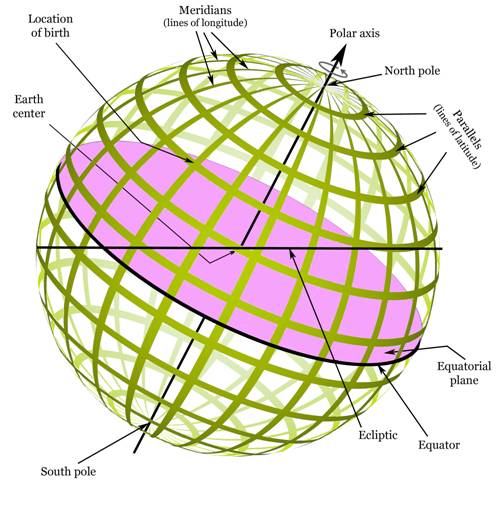
Next, we will add the birth location on the earth's surface. This is shown in the diagram below.

I've picked a birth location at Washington, DC, U.S.A that is at a latitude of about 39° North. The time is 10:45 a.m. on May 5, 1990.

How do we know the diagram below corresponds to a birth time in the morning and not the afternoon?

Imagine observing the Earth spinning around its polar axis (counterclockwise when viewed from above the North Pole) for several hours. The birth location is fixed to the point on the earth's surface at the designated lines of latitude and longitude depicted in the diagram below. As time moves forward, you will see the birth location move toward the right (and initially down a bit) until eventually, the birth point moves to the far right side of the Earth. This would correspond to sunset at this birth point time. As the Earth continues to rotate, the birth point will be behind the Earth, and receive no sunlight. Eventually this birth point will appear on the far left side of the Earth, which corresponds to sunrise at this birth point time. In a few more hours, it will come back to the same position as shown in the diagram below.

With this understanding, you can see that the birth point time was in the morning as it is on the left side of the Earth from our vantage point at the Sun.
 

 

 

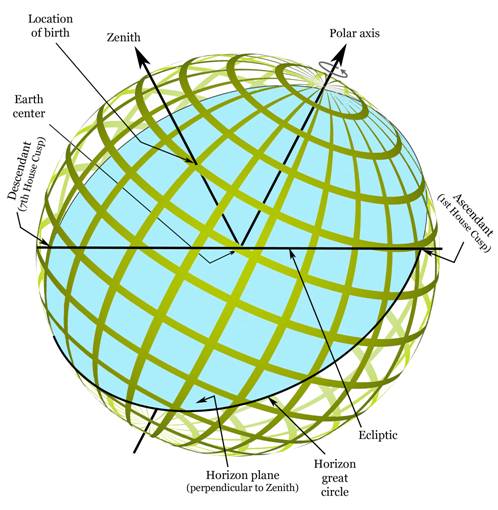
Zenith and Horizon Plane

The next line we will add is the Zenith. This is a line pointing straight up at the location of birth.

In the diagram below, the Zenith is depicted as a line originating at the earth's center and passing through the earth's surface at the location of birth. From the perspective of the person born at this location, the Zenith would appear as a line straight up toward the center of the visible sky.

The Zenith is perpendicular to the earth's surface. The plane formed by the horizon at the place of birth is referred to as the Horizon plane and is shown in the diagram below.

Geocentric Geometry

Calculations performed by astrology software programs are Earth-centered. Specifically, the birth location is moved to the earth's center. Then the calculations are performed from this new location. This simplifies the algorithms used to create a Natal chart. The error created by this repositioning of the birth location is negligible since  the Planets are so far away from the Earth.

To accomplish this, we will move the Horizon plane to the earth's center without changing its orientation (perpendicular to the Zenith). This is shown on the diagram below. I've also added a label for the Horizon great circle, which is the circle around the earth's surface formed by the Horizon plane.

 

Since this diagram is getting messy, I've eliminated the equator and equatorial plane as it no longer serves us going forward. This simplified diagram is below.

 

Ascendant A^s and Descendant D^s

We can now identify the points for the Ascendant A^s and Descendant D^s. These are the two points on the earth's surface where the Horizon great circle intersects the Ecliptic. I've added these points in the diagram below. On the right side is the Ascendant A^s and on the left side is the Descendant D^s. Observe that the Descendant D^s is behind the Earth from our vantage point.

Zenith-Ascendant Plane

We will create one last plane, which is the Zenith-Ascendant plane. This is a plane that passes through three points: the earth's center, the location of birth, and the Ascendant A^s (and the Descendant D^s by default). This is shown on page 222.

To put the Zenith-Ascendant plane in perspective, imagine standing at the birth location and pointing straight up along the Zenith. Now sweep your arm 90° to the Ascendant A^s on the eastern horizon. You just formed a 90° arc along the Zenith-Ascendant great circle. Similarly, you can point straight up along the Zenith, and sweep your arm 90° to the Descendant D^s on the western horizon. That will also form a 90° arc on the Zenith-Ascendant great circle.

Viewing a close-up at the birth location in the diagram on page 222, you see that the Zenith-Ascendant great circle does not go exactly east and west along the parallel (line of latitude), but deviates somewhat north of due east and south of due west. The Zenith-Ascendant great circle orientation varies during the day. Sometimes it points north of east, and at other times south of east.
 

 

 

 

 

Midheaven M^c

We now have the points for the Ascendant A^s (1^st House Cusp) and the Descendant D^s (7^th House Cusp). Next, we will locate the Midheaven M^c (10^th House Cusp), which will in turn also define the Imum Coeli I^c (4^th House Cusp) since the Imum Coeli I^c is opposite the Midheaven M^c.

The diagram below shows how we find the Midheaven M^c. We start at the location of birth and follow the north-south meridian line in a southerly direction until we intersect the Ecliptic. That point on the Ecliptic defines the Midheaven M^c. By default, we have also defined the Imum Coeli I^c, which is 180° from the Midheaven M^c.

Up to this point, we have not talked about House systems because all House systems define the Ascendant A^s (and by default, the Descendant D^s) and the Midheaven M^c (and by default, the Imum Coeli I^c) the same way.

Defining the intermediate Cusps (2^nd, 3^rd, 5^th, 6^th, 8^th, 9^th, 11^th,, and 12^th House Cusps) is done differently by the varying House systems.

In the next part of this chapter, we will look at how the Krusiński House system defines the intermediate Cusps. As you will see shortly, the methodology used to determine the intermediate House Cusps using the Krusiński system is the same method we used to determine the Midheaven M^c. Fortunately, we will not need to create any new planes in order to proceed forward. We already have everything we need.

 

 

 

Krusiński House System

With the Krusiński House system, we begin by taking the 90° arc from the Zenith to the Ascendant A^s on the Zenith-Ascendant great circle and dividing it into three 30° segments. Likewise, we take the 90° arc from the Zenith to the Descendant D^s and also divide it into three 30° segments. You can see this in the diagram below.

From the perspective of the birth location, we are forming a 90° arc by pointing straight up (Zenith) and sweeping our arm toward the eastern horizon to the Ascendant A^s. We then divide this 90° arc into three equal arcs of 30°. We've now divided the left half of the visible sky (viewed from the birth location facing south) into three equal portions.

We follow the same procedure to divide the right portion of the visible sky into three equal portions by pointing straight up (Zenith) and sweeping our arm toward the western horizon to the Descendant D^s to form a 90° arc. We then divide this 90° arc into three equal arcs of 30°. We now have the visible sky divided into six equal portions. The portion of the sky behind the Earth is, by default, also divided into six equal 30° portions.

To calculate the intermediate House Cusps, we follow the same procedure as we did to determine the Midheaven M^c. That is, we take the points along the Zenith-Ascendant great circle where the 30° arcs intersect this great circle, and follow each along the north-south meridian line until we intersect the Ecliptic. This is depicted in the diagram on page 227.
 

 

 

 

 

 

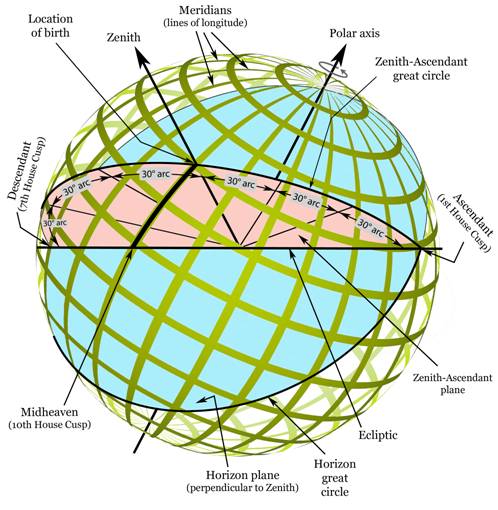
We now have located the 8^th, 9^th, 11^th, and 12^th House Cusps (and by default the 2^nd, 3^rd, 5^th, and 6^th House Cusps).

Other House systems such as Koch and Placidus, determine the House Cusps by dividing the arc along the Ecliptic between the Ascendant A^s and the Midheaven M^c into three segments using parallel arcs to obtain the 11^th and 12^th House Cusps (and the 5^th and 6^th by default), and dividing the arc along the Ecliptic between the Midheaven M^c and the Descendant D^s into three segments to obtain the 8^th and 9^th House Cusps (and the 2^nd and 3^rd by default).

This approach seems incongruous to me because, in general, the angle of the arc along the Ecliptic between the Midheaven M^c and the Ascendant A^s is not 90°. For example, this angle is roughly 106° in the diagram on the previous page. The arc between the Midheaven M^c and the Descendant D^s is 74°. Later, I'll show you how I figured this out. Attempting to use formulations on an arc that is already distorted due to an earlier projection is still going to result in distortions.

Until I became aware of the Krusiński House system, I was uneasy in my astrology practice with all the House systems. It made no sense to me that the 3-D sky from the perspective of the birth location should be distorted using methods that deviated from the simplicity and beauty of all the other geometry associated with the Natal chart. I am comfortable and confident in the Krusiński House system because it is geometrically simple, uses a methodology consistent with the calculation of the Midheaven M^c (which everyone agrees with), and divides the visible sky into equal portions without distortion.
Sun on the Ecliptic

Before looking at the 2-D Natal chart that corresponds to the 3-D celestial diagram we created, we need to add one more very important point: where the Sun intercepts the Ecliptic.

We find the intercept of the Sun on the Eclipse by determining where the line from the center of the Sun to the center of the Earth intersects the Ecliptic. Our vantage point in the 3-D celestial diagram is at the sun's center. Because of this, the Sun intercepts the Ecliptic at the same point on the 3-D celestial diagram as the earth's center. This is shown in the diagram below. Please take the time to find this point as it is important for our next step.

Shortly, we will want to view the 2-D Natal chart from the same vantage point as the 3-D celestial diagram. To do this, we will need to find the points on the Natal chart that include our vantage point (sun's center), where the Sun intercepts the Ecliptic, and the earth's center.

Viewing the locations of the 10^th and 11^th House Cusps in the 3-D celestial diagram below, notice that the Sun intercepts the Ecliptic in the 10^th House and is very close to the 11^th House Cusp.

Now we will contrast the 3-D celestial diagram (below) with the 2-D Natal chart (second diagram below).
 

3-D Celestial Diagram versus 2-D Natal Chart

Now we want to view both the 3-D (three-dimensional) celestial diagram and the 2-D (two-dimensional) Natal chart from the same vantage point (two diagrams above). Then we can make comparisons.

The center of a Natal chart represents the earth's center. The Ecliptic is represented by one of the outermost rings as marked in the Natal chart above. The positions of the Planets in the Natal chart indicate where the Planets cross the Ecliptic. The actual Planets are somewhere far outside the Natal chart. For example, the Sun intercepts the Ecliptic where the Sun is located in the Natal chart. The actual Sun is outside the Natal chart as depicted in the Natal diagram above.

Now, rotate the Natal chart so you are looking along the arrow from the Location of the Sun point (sun's center) to the center of the chart (earth's center). You are now looking at the 2-D Natal chart from the same vantage point as the 3-D celestial diagram. Notice the Sun intercepts the Ecliptic in the 10^th House near the Cusp of the 11^th House in both the Natal chart and the 3-D celestial diagram.

Viewing the Natal chart from the same vantage point as the 3-D celestial diagram, observe that the 10^th House Cusp line (Midheaven M^c) is to your left and points down and to the left. In the 3-D celestial diagram, this is equivalent to the north-south meridian line going from the Zenith to the Midheaven M^c. Notice that this line also points down and to the left.

The black line I added to the Natal chart that is perpendicular to the shaded bar represents the dividing line between night and day on Earth. Since the shaded bar from the Sun to the earth's center is perpendicular to this line, the half of the Natal chart closest to you  (from the vantage point of the sun's center) will be bathed in sunlight, while the back half will receive no sunlight. Observe that the Ascendant A^s is receiving sunlight. In the 3-D celestial diagram, the Ascendant A^s is visible on the earth's surface, which means it is likewise receiving sunlight. The Descendant D^s in the Natal chart is in darkness because it is behind the black line perpendicular to the shaded line. Thus it is behind the Earth from the vantage point of the Sun. You can see that this is the case when viewing the Descendant D^s in the 3-D celestial diagram.

Earlier in this chapter, I mentioned that the angle along the Ecliptic from the Midheaven M^c to the Ascendant A^s is 106° and from the Midheaven M^c to the Descendant D^s is 74°. Here's how we figure it out. Viewing the Natal chart above, we see that the Midheaven M^c is at 8° 5' Aries a, the Ascendant A^s at 23° 54' Cancer f, and the Descendant D^s is at 23° 54' Capricorn z. You can determine these two angles by calculating the angular distance from the Midheaven M^c to the Ascendant A^s, and the Midheaven M^c to the Descendant D^s. I'll leave it up to you to do the math.

If you were able to follow along in this chapter, you now have a better appreciation of how the 2-D Natal chart depicts the 3-D configuration of the Sun and Earth at birth.

In the next chapter, we will take a look at the popular House systems and compare the effects on the intermediate House Cusps. [see the book]